算法-动态规划

### 97.交错字符串

给定三个字符串 s1、s2、s3，请你帮忙验证 s3 是否是由 s1 和 s2 交错 组成的。

两个字符串 s 和 t 交错 的定义与过程如下，其中每个字符串都会被分割成若干 非空 
	子字符串

- `s = s1 + s2 + ... + sn`
- `t = t1 + t2 + ... + tm`
- `|n - m| <= 1`
- `交错 是 s1 + t1 + s2 + t2 + s3 + t3 + ... 或者 t1 + s1 + t2 + s2 + t3 + s3 + ...`

> 注意：a + b 意味着字符串 a 和 b 连接。

示例 1：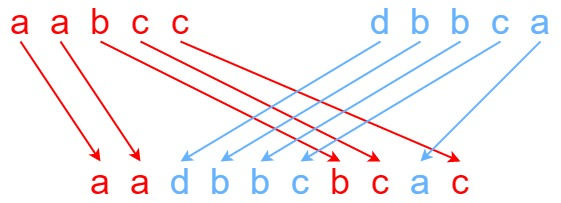

![](https://i-cooltea.top/usr/uploads/2024/03/3057182419.png)

输入：s1 = "aabcc", s2 = "dbbca", s3 = "aadbbcbcac"
	输出：true

示例 2：

输入：s1 = "aabcc", s2 = "dbbca", s3 = "aadbbbaccc"
	输出：false

示例 3：

输入：s1 = "", s2 = "", s3 = ""
	输出：true

解决这个问题的正确方法是动态规划。

1.
首先如果  $$|s_1| + |s_2| \neq |s_3|$$
那 $$ s_3$$ 必然不可能由 $$ s_1 $$ 和 $$ s_2 $$ 交错组成。

2.
若  $$|s_1| + |s_2| = |s_3|$$ 时，我们可以用动态规划来求解。
我们定义 $$ f(i,j)$$  表示 $$s_1$$ 的前 $$i$$ 个元素 
和 $$s_2$$   的前 $$j$$ 个元素是否能交错组成 $$s_3$$  的前 $$ i+j $$ 个元素。

3.
如果 $$s_1$$  的第 $$i$$ 个元素和 $$s_3$$ 的第 $$ i+j $$ 个元素相等，
那么 $$s_1$$  的前 i 个元素和 $$s_2$$ 的前 j 个元素是否能交错组成 $$s_3$$ 的前 
$$i+j$$ 个元素取决于 $$s_1$$  的前 $$ i - 1 $$ 个元素和 $$ s_2 $$ 的前 $$ j $$ 
个元素是否能交错组成 $$ s_3 $$  的前 $$ i + j + 1 $$ 个元素，

4.
由此推导出动态规划的转移方程

即 $$ f(i,j) $$,  取决于 
$$ f(i-1,j) $$ 与 $$s_1 [i] == s_3[i+j-1]$$  ,
$$ f(i,j-1) $$ 与 $$s_2 [j] == s_3[i+j-1]$$  ,
两者为或的关系, 只要有一项成立 $$f(i,j)$$ 即为真值

边界条件为 $$ f(0,0) = True $$

```Go

// 版本1
func isInterleave(s1 string, s2 string, s3 string) bool {
	len1 := len(s1)
	len2 := len(s2)
	len3 := len(s3)
	if len1+len2 != len3 {
		return false
	}
	dp := make(map[[2]int]bool)

var isCorrectSeq func(i, j int) bool
	isCorrectSeq = func(i, j int) bool {
		key := [2]int{i, j}
		if i < 0 || j < 0 || i == 0 && j == 0 {
			return true
		} else if val, ok := dp[key]; ok {
			return val
		}

result := false
		if i > 0 && s1[i-1] == s3[i+j-1] && isCorrectSeq(i-1, j) ||
			j > 0 && s2[j-1] == s3[i+j-1] && isCorrectSeq(i, j-1) {
			result = true
		}
		dp[key] = result

return dp[key]
	}

return isCorrectSeq(len1, len2)
}

// 版本2
func isInterleave(s1 string, s2 string, s3 string) bool {    
    if len(s1) + len(s2) != len(s3) {
        return false
    }
    n := len(s2)

dp := make([]bool, n+1)
    dp[0] = true

for i := 0; i <= len(s1); i++ {
        for j := 0; j <= len(s2); j++ {
            p := i + j - 1
            if i > 0 {
                dp[j] = dp[j] && (s1[i-1] == s3[p])
            }

if j > 0 {
                dp[j] = dp[j] || (dp[j-1] && s2[j-1] == s3[p])
            }
        }
    }

return dp[n]
}
```

> 此处版本1为上述思路的实现, 
版本2为LeetCode 上其他网友发布的答案 
仔细对照两个版本的代码, 版本2 为更优解
存在以下几点优势 : 
1. 利用迭代替代递归调用避免了函数调用栈的开销
2. 一维数组dp来保存中间结果, 更能节省空间 
3. 比较简洁, 可读性高

清凉的茶 · i-cooltea

评论已关闭

标签

链接

其它